|
Monte Carlo Experiments: "Drunken Sailor's" Random Walk
Theory
A prerequisite for the implementation of a stochastic approach is the availability of a very fast computer, which will perform many random trials or simulations with subsequent treatment of a large amount of numerical data. A second prerequisite is an unlimited supply of random numbers, with a known distribution function. Calculations based on the use of random numbers are generally known (for obvious reasons) as Monte Carlo experiments. The Monte Carlo approach is not limited to probabilistic calculations but can also be used for performing mathematical calculations (such as integration of complicated functions), which are otherwise difficult or impossible to be carried out by conventional techniques.
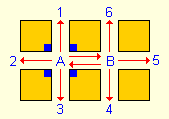
The "Drunken Sailor" problem The "drunken sailor" problem can serve as an introductory example on Monte Carlo experiments. The problem is as follows: Consider a town consisting of 3x2 blocks shown below.
A "drunken sailor" stands in one of the two crossroads and he wants to leave the town. Since the sailor is very drunk, the probabilities of travelling up, down, left or right are equal. What is the probability for the sailor to reach each one of the six town exits? Considering the small number of exits and crossroads, this problem can be solved easily by a deterministic approach, as follows Starting from crossroad A the probability to move to each one of the exits 1, 2, 3, or to the next crossroad B is obviously 1/4. Supposing that the sailor has moved to crossroad B, then again the probability to move to each one of the exits 4, 5, 6, or back to crossroad A is again 1/4, therefore 1/4 of the initial probability to be found there, i.e. 1/4(1/4) = 1/42. Again, supposing that he has returned to crossroad A the probability to move to each one of the exits 1, 2, 3, or back to crossroad B are 1/4(1/42) = 1/43 and so on. Therefore, by summing up the probabilities for each exit, we have: Probability for each one of the exits 1, 2, 3:
Probability for each one of the exits 4, 5, 6:
For a 4x2 or 3x3 town, the problem can be solved similarly, but more tedious calculations are required. But what about for an even larger "town" with blocks arranged into a regular (rectangular shape) or (even worst) into an irregular (partially filled) array formation? Here comes the Monte Carlo experiment (performed with a computer) to the rescue. The program simulates the town and the direction of the sailor's movement is chosen by using the random number generator of the programming platform. Actually, these numbers are "pseudorandom" because there is nothing non-deterministic in computer programs. Thousands or millions of "sailor's walks" (N) are simulated and the sailor's arrivals (nj) to each exit (j = 1,2,..) are counted. An estimate of the probability of the sailor to leave the town from exit j is simply the quotient nj/N. This estimate becomes more accurate as the number of N increases, but it will acquire exactly the correct value only after an infinite number of simulations. This simulation can be expanded to a "3-dimensional town" i.e. the space. In chemistry, the "sailor" may be a molecule moving randomly with a certain average speed under the influence e.g. of diffusion. Instead of a town we could have a chamber or a porous material of given geometry. The problem could be the estimation of the concentration of a gaseous compound diffused from a certain point or area, in a given segment of the space after a fixed time. The model can be expanded by taking into account phenomena like collisions between molecules (a large number of molecules are travelling at the same time) and/or adsorption. Provided, of course, that we have the appropriate program for performing the simulation, the only price to be paid for this kind of calculations is computer time. The more computer time we spend, the more accurate the results are.
Applet This applet demonstrates the simple "Drunken Sailor's" random walk problem. Since there is only one sailor, no collisions are to be taken into account. The user can choose the size of the "town" (up to a 15x12 blocks) by clicking buttons X+, X-, Y+, and Y-. The user has only to click and mark the "starting" crossroad and then to click button "START". If "slow" or "fast" speed has been selected (by clicking on the corresponding radiobuttons) the user can observe the movements of the "sailor". The current estimates of probabilities are shown on each "town" exit. At the lower part of the applet screen are the number of simulations performed so far and the average distance travelled by the sailor are also shown. As the number of simulations increases the probabilities shown at each exit tend to acquire almost constant values. When animation is active the program runs very slowly, in order to observe the sailor's movements. In actual simulations no animations are needed. By selecting "No animation" the animation is suspended and simulations run much faster. It should be stressed that with a powerful mainframe computer simulations like the present one can be performed at rates of few millions per second. It is of interest to note, how fast the probabilities converge to the theoretical value 0.25 for a 2x2 town, or to the as above calculated probabilities for a 3x2 town.
|
The calculation of
certain quantities, such as the probabilities of occurrence of certain events
within a given segment of time and/or space, sometimes is either difficult or
even impossible to be carried out by a deterministic
approach, i.e. by using or by
deriving closed form equations describing the phenomenon under
investigation. In these cases,
the possibility of performing the required calculations by a
non-deterministic or stochastic approach, is
examined.
