Diffusion Controlled Electrode Processes
 

Theory

In voltammetry, the working electrode can be considered as a medium whose reductive or oxidative power can be externally adjusted by the magnitude of the imposed potential. When its potential is decreased or increased (algebraically) it becomes stronger reductant or oxidant, respectively.

Therefore, the working electrode (usually consisting of a chemically inert conductive material such as Pt) acts as a simple donor or acceptor of electrons participating in the general electrode reaction

where O and R are the oxidized and the reduced forms of an electroactive substance (e.g. O = Fe³⁺, R = Fe²⁺,  n=1).

The magnitude and the direction of the current passing through the electrode are indicative of the rate of the electrode reaction and of its prevailing direction.

In essence, any electrode reaction is a heterogeneous redox reaction. If its rate depends exclusively on the rate of mass transfer, then we have a mass-transfer controlled electrode reaction. If the only mechanism of mass transfer is diffusion (i.e. the spontaneous transfer of the electroactive species from regions of higher concentrations to regions of lower concentrations), then we have a diffusion controlled electrode reaction.

Diffusion controlled electrode reactions embrace the majority of electrode reactions usually encountered in voltammetry and their mathematical treatment is relatively simple.

Diffusion Equations (Fick's laws)

The Fick's 1st law states that the flux J_A(x,t) of substance A due to diffusion at time t (usually expressed in mol / cm² s) and position x is proportional to the concentration gradient ∂C_A(x,t)/∂x

and depends on the diffusion constant D_A of species A. The minus sign indicates that the direction of flux is opposite to the direction of the gradient.

The concentration gradient and the resulting flux (across x-axis) is depicted in the figure below. The diagram in the lower part is the concentration profile of the diffusion-driven substance across axis-x.

Time is introduced as a variable in Fick's 2nd law. We suppose that at x = 0 there is the surface of the working electrode and the concentration of A is initially the same at any distance x. At t = 0 the electrode potential is stepped to a value that practically makes zero the concentration of A at the surface of the electrode (x = 0). Then, the concentration of A, the distance x and time t are interconnected through the following differential equation: 

If initially (t = 0) solution contains only species O at a concentration [O]* [* denotes the concentration in the bulk of the solution], then their concentration profiles are shown in the figure below (left). After stepping the potential at a value where practically all O in contact with the electrode is reduced to R, then typical concentration profiles of O and R at t₁ < t₂ < t₃ are shown (right). These curves are the graphical representations of the functions-solutions of the last differential equation and they are indicative of the gradual expansion of the so-called diffusion layer towards the bulk of the solution. Obviously, it is always [O]+[R] = [O]* at any t and x.

Effect of Electrode Potential

If the electrode reaction is completely reversible, then the ratio [O]_x=0/[R]_x=0 on the surface of the working electrode (x=0) at any time (t>0) depends exclusively on its potential (E) and it can be calculated by Nernst's equation

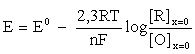
or (if we define ΔE = E - E⁰)

It is obvious that the ratio [O]_x=0/[R]_x=0 is an exponential function of nΔE. Indicative values of this ratio  for various nΔE values (at room temperatures) are shown in the table below.

In the figure below  the concentration profiles of O and R are shown (at a given time instance, t>0) for the values nΔE given in the previous table.

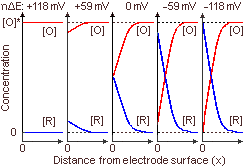
Therefore at oxidative potentials (e.g. at nΔE ³ +118 mV), the electrode remains practically in equilibrium with [O] species, whereas at much lower potentials (e.g. at nΔE £ -118 mV), practically the whole quantity of O in contact with the electrode is reduced to R. During the reduction of O to R we observe a flow of cathodic current. This current is gradually diminished (to almost zero), as a result of the gradual expansion of the diffusion layer towards the solution bulk, which in turn will gradually decrease (according to Fick's 1st law) the flux of O species towards the electrode surface.

Applet

In this applet a simulation of diffusion controlled reversible electrode reaction is performed. We can observe the movements and the state (O or R) of the electroactive particles during this reaction. We can also observe the effect of the potential applied to the working electrode.

The user may select which particles (O, R or both) appear on display ("Species Shown"). In addition, the number of particles ("Number of particles", 2000, 5000 or 10000)  used in the simulation can also be selected. The greater this number is, the more precise the concentration profiles are, but the simulation advances much more slowly.

The user can accelerate the simulation by selecting the number of simulation steps before each redisplaying of the particles and of the concentration profiles ("New frame after": 1, 3, 10 steps).

Initially, the only existing particles are those of the oxidized form (O), which move randomly to any direction with a given mean velocity. The electrode potential is the standard reduction potential E = E⁰ (or nΔE=0) of the half-reaction

At this potential value (where [O]_x=0 / [R]_x=0 = 1), when a particle (either O or R) contacts the electrode surface has a 50% chance to be converted to either form (O or R). In the lower diagram, the corresponding profiles are shown. When nΔE =0, after an extended period of time both concentrations [O] and [R] will become equal at any distance.

We can observe the effect of changing E on concentration profiles. For nΔE = -59 mV, when a particle contacts the electrode it has an about 91% chance to become R and a 9% chance to become O, whereas for nΔE = -118 mV, these chances are 99% and 1%, respectively. Therefore, for n = -118 mV or lower, after an extended period of time, practically all particles will be reduced to R.

Similarly, for nΔE = +59 mV, when a particle contacts the electrode it has an about 91% chance to become O and a 9% chance to become R, whereas for nΔE = +118 mV, the chances are 99% and 1%, respectively. Therefore, for n = +118 mV or higher, after an extended period of time, practically all particles will be oxidized to O.

It is of interest to observe the formation of quickly dispersed concentration zones, by imposing periodic changes of nΔE during the electrode reaction, simulating cyclic voltammetry or step-potential experiments

It is also possible to evaluate the direction and the value of the electric current (flowing through the cell) as a numerical indication appearing in an edit box ("Net Charge per Frame"). This number is equal to the net number of electrons transferred from the electrode to particles O for their reduction to R (negative indication) or from particles R to electrode after their oxidation to O (positive indication).